(本小题10分)
对于函数f（x）（x
）恒有f（ab）=f（a）+f(b)且x＞1时f（x）＞0 ，f（2）=1
(1)求f（4）、f（1）、f（-1）的值；
(2)求证f（x）为偶函数；
(3)求证f（x）在（0，+
）上是增函数；
(4）解不等式f（x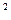
-5）＜2.
推荐套卷
(本小题10分)
对于函数f（x）（x）恒有f（ab）=f（a）+f(b)且x＞1时f（x）＞0 ，f（2）=1
(1)求f（4）、f（1）、f（-1）的值；
(2)求证f（x）为偶函数；
(3)求证f（x）在（0，+）上是增函数；
(4）解不等式f（x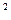-5）＜2.
粤公网安备 44130202000953号