如图所示，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=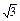
，
BC=1，PA=2，E为PD的中点.
（1）求直线AC与PB所成角的余弦值；
（2）在侧面PAB内找一点N，使NE⊥平面PAC，并求出N点到AB和AP的距离.
相关试题
，定义面积函数
为直线
与
的值为（）
和
是函数
的两个极值点，其中
.
的取值范围；
，求
的最大值（注:
是自然对数的底数）.
上函数
对任意正数
都有
，当
时，
，且
.
的值；
的不等式
.
.
时，求满足
的实数
的范围；
对任意的
恒成立，求实数
的范围.
，且函数
在
处取到最大值
，
的取值范围；
的最小值.推荐套卷
如图所示，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，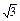
BC=1，PA=2，E为PD的中点.
（1）求直线AC与PB所成角的余弦值；
（2）在侧面PAB内找一点N，使NE⊥平面PAC，并求出N点到AB和AP的距离.
粤公网安备 44130202000953号