已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1与l2的距离是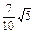 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:
①P是第一象限的点;②P点到l1的距离是P点到l2的距离的 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是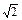 ∶
∶ .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
相关知识点
推荐套卷
已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1与l2的距离是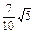 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:
①P是第一象限的点;②P点到l1的距离是P点到l2的距离的 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是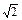 ∶
∶ .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.