(本小题满分12分)
某单位组织50名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,创导文明新风;2、到指定的社区、车站、码头做义工,帮助那些需要帮助的人。各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
|
宣传慰问
|
义工救助
|
总计
|
20至40岁
|
11
|
16
|
27
|
大于40岁
|
15
|
8
|
23
|
总计
|
26
|
24
|
50
|
(Ⅰ) 用分层抽样方法在做义工的志愿者中随机抽取6名,大于40岁的应该抽取几名?

(Ⅱ) 在上述抽取的6名志愿者中任取2名,求恰有1名志愿者年龄大于40岁的概率.
(Ⅲ)如果“宣传慰问”与“做义工”是两个分类变量,并且计算出随机变量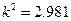 ,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?