(本小题满分12分)
某校学生会进行了一次关于“消防安全”的调查活动,组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查.活动结束后,团委会对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
年龄(岁)
|
[10,20)
|
[20,30)
|
[30,40)
|
[40,50)
|
[50,60)
|
[60,70]
|
频数
|
m
|
n
|
14
|
12
|
8
|
6
|
知道的人数
|
3
|
4
|
8
|
7
|
3
|
2
|
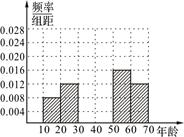
(Ⅰ)求上表中的m、n的值,并补全右图所示的的频率直方图;
(Ⅱ)在被调查的居民中,若从年龄在[10,20),[20,30)的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.