某校有5名学生报名参加义务献血清治疗重症甲流患者活动, 这5人中血型为A型的2名, 血型为B型的学生1 名,血型为O型的学生2名,已知这5名学生中每人符合献血条件的概率均为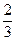
（1）若从这5名学生中选出2名,求所选2人血型为O型或A型的概率
（2）求这5名学生中至少有2名学生符合献血条件的概率.
，画出程序框图．
的算法，画出算法的程序框图.相关知识点
推荐套卷
某校有5名学生报名参加义务献血清治疗重症甲流患者活动, 这5人中血型为A型的2名, 血型为B型的学生1 名,血型为O型的学生2名,已知这5名学生中每人符合献血条件的概率均为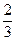 （1）若从这5名学生中选出2名,求所选2人血型为O型或A型的概率
（2）求这5名学生中至少有2名学生符合献血条件的概率.
粤公网安备 44130202000953号