已知椭圆C的中点在原点，焦点在x轴上，离心率等于
，它的一个顶点恰好是抛物线
的焦点．
(1)求椭圆C的方程;
(2)点P(2，3)，Q(2，-3)在椭圆上，A、B是椭圆上位
于直线PQ两侧的动点，
(i)若直线AB的斜率为，求四边形APBQ面积的最大值;
(ii)当A、B运动时，满足∠APQ=∠BPQ，试问直线AB的斜率是否为定值，请说明理由．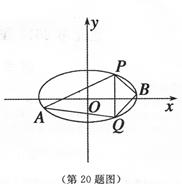
相关试题
的端点为
，直线
，使
，求
的值．
，使得复数
分别满足下列条件，若存在，求出
的前
项和为
，已知
，
.
的值；
.
的前
项和为
，且满足
的前
，求
－1)海里的C处的缉私船奉命以10
推荐套卷
已知椭圆C的中点在原点，焦点在x轴上，离心率等于，它的一个顶点恰好是抛物线的焦点．
(1)求椭圆C的方程;
(2)点P(2，3)，Q(2，-3)在椭圆上，A、B是椭圆上位
于直线PQ两侧的动点，
(i)若直线AB的斜率为，求四边形APBQ面积的最大值;
(ii)当A、B运动时，满足∠APQ=∠BPQ，试问直线AB的斜率是否为定值，请说明理由．
粤公网安备 44130202000953号