已知椭圆C的中心在原点，左焦点为F1，其右焦点F2和右准线分别是抛物线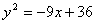
的顶点和准线.
⑴求椭圆C的方程；
⑵若点P为椭圆上C的点，△PF1F2的内切圆的半径为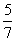
，求点P到x轴的距离；
⑶若点P为椭圆C上的一个动点，当∠F1PF2为钝角时求点P的取值范围.
．
推荐套卷
已知椭圆C的中心在原点，左焦点为F1，其右焦点F2和右准线分别是抛物线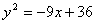的顶点和准线.
⑴求椭圆C的方程；
⑵若点P为椭圆上C的点，△PF1F2的内切圆的半径为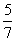，求点P到x轴的距离；
⑶若点P为椭圆C上的一个动点，当∠F1PF2为钝角时求点P的取值范围.
粤公网安备 44130202000953号