(本小题满分14分)已知函数 的导函数是
的导函数是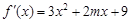 ,
, 在
在 处取得极值,且
处取得极值,且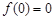 ,
,
(1)求 的极大值和极小值;
的极大值和极小值;
(2)记 在闭区间
在闭区间 上的最大值为
上的最大值为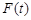 ,若对任意的
,若对任意的
 总有
总有 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)设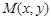 是曲线
是曲线 上的任意一点.当
上的任意一点.当 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
推荐套卷
(本小题满分14分)已知函数 的导函数是
的导函数是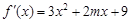 ,
, 在
在 处取得极值,且
处取得极值,且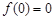 ,
,
(1)求 的极大值和极小值;
的极大值和极小值;
(2)记 在闭区间
在闭区间 上的最大值为
上的最大值为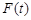 ,若对任意的
,若对任意的
 总有
总有 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)设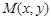 是曲线
是曲线 上的任意一点.当
上的任意一点.当 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.