建立极坐标系证明：已知半圆直径|AB|=2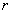
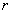（>0），半圆外一条直线
与AB所在直线垂直相交于点T，并且∣AT|=2
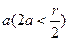.若半圆上相异两点M.N到的距离|MP|，|NQ|满足|MP|∶|MA|=|NQ|∶|NA|=1，则|MA|+|NA|=|AB|.
相关试题
中，
是边长为
的正三角形，平面
平面
，四边形
，
是
的中点，
是
的中点.
平面
.
的余弦值.
满足
．
，
，
，
，并由此猜想通项公式
；
，
.
；
恒成立的充分条件是
，求实数
的取值范围．
的通项公式为
，其前
项和为
.
及
的表达式；
，求数列
的前
；
，令
，求
的取值范围.
的最大值为
．
的值；
的单调递增区间；
个单位，得到函数
的图象，求函数
上的最大值和最小值．相关知识点
推荐套卷
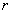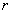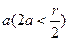建立极坐标系证明：已知半圆直径|AB|=2（>0），半圆外一条直线与AB所在直线垂直相交于点T，并且∣AT|=2.若半圆上相异两点M.N到的距离|MP|，|NQ|满足|MP|∶|MA|=|NQ|∶|NA|=1，则|MA|+|NA|=|AB|.
粤公网安备 44130202000953号