若关于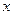 的实系数方程
的实系数方程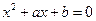 有两个根,一个根在区间
有两个根,一个根在区间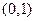 内,另一根在区间
内,另一根在区间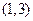 内,记点
内,记点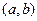 对应的区域为
对应的区域为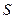 .
.
(1)设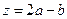 ,求
,求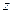 的取值范围;
的取值范围;
(2)过点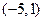 的一束光线,射到
的一束光线,射到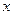 轴被反射后经过区域
轴被反射后经过区域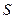 ,求反射光线所在直线
,求反射光线所在直线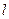 经过区域
经过区域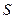 内的整点(即横纵坐标为整数的点)时直线
内的整点(即横纵坐标为整数的点)时直线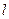 的方程.
的方程.
推荐套卷
若关于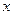 的实系数方程
的实系数方程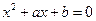 有两个根,一个根在区间
有两个根,一个根在区间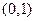 内,另一根在区间
内,另一根在区间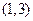 内,记点
内,记点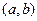 对应的区域为
对应的区域为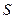 .
.
(1)设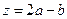 ,求
,求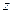 的取值范围;
的取值范围;
(2)过点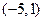 的一束光线,射到
的一束光线,射到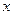 轴被反射后经过区域
轴被反射后经过区域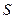 ,求反射光线所在直线
,求反射光线所在直线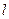 经过区域
经过区域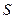 内的整点(即横纵坐标为整数的点)时直线
内的整点(即横纵坐标为整数的点)时直线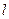 的方程.
的方程.