(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
我们把定义在 上,且满足
上,且满足 (其中常数
(其中常数 满足
满足 )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数 满足
满足 且图像关于直线
且图像关于直线 对称.求证:函数
对称.求证:函数 是偶函数;
是偶函数;
(2)当 时,某个似周期函数在
时,某个似周期函数在 时的解析式为
时的解析式为 ,求函数
,求函数 ,
, 的解析式;
的解析式;
(3)对于确定的 时,
时, ,试研究似周期函数函数
,试研究似周期函数函数 在区间
在区间 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
相关知识点
推荐套卷
 的前
的前 项和记为
项和记为 ,点
,点 在直线
在直线 ,
, .
. 为何值时,数列
为何值时,数列 是数列
是数列 的前
的前
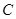 的两焦点分别为
的两焦点分别为 ,长轴长为6.
,长轴长为6.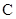 的标准方程;
的标准方程; 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆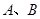 两点,求线段
两点,求线段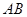 的长度.
的长度.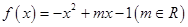 .
. 在区间
在区间 上的最大值;
上的最大值;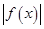 在区间
在区间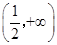 上单调递增,试求m的取值范围.
上单调递增,试求m的取值范围. 分别是
分别是 中角
中角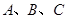 的对边,且
的对边,且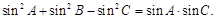
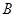 的大小;
的大小;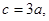 求
求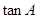 的值.
的值.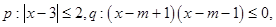 若
若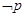 是
是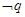 的充分而不必要条件,求实数m的取值范围.
的充分而不必要条件,求实数m的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号