已知二次函数y=f(x)在x=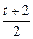
处取得最小值－
(t＞0),f(1)=0.
(1)求y=f(x)的表达式；
(2)若任意实数x都满足等式f(x)·g(x)+anx+bn=xn+1［g(x)］为多项式，n∈N*),试用t表示an和bn；
(3)设圆Cn的方程为(x－an)2+(y－bn)2=rn2，圆Cn与Cn+1外切(n=1,2,3,…);{rn}是各项都是正数的等比数列，记Sn为前n个圆的面积之和，求rn、Sn.
相关试题
，且
．
在区间
上有零点，求实数
的取值范围；
上的最大值是2，求实数
，
．
时，求
的最大值和最小值；
，求
的取值范围．
中，点
在线段
上，且
，延长
到
，使
．设
．
表示向量
；
与
共线，求
的值．
，
．
，求
的值；
，求
的单调递增区间．
．
时，求
；
，求
的取值范围．推荐套卷
已知二次函数y=f(x)在x=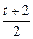处取得最小值－ (t＞0),f(1)=0.
(1)求y=f(x)的表达式；
(2)若任意实数x都满足等式f(x)·g(x)+anx+bn=xn+1［g(x)］为多项式，n∈N*),试用t表示an和bn；
(3)设圆Cn的方程为(x－an)2+(y－bn)2=rn2，圆Cn与Cn+1外切(n=1,2,3,…);{rn}是各项都是正数的等比数列，记Sn为前n个圆的面积之和，求rn、Sn.
粤公网安备 44130202000953号