已知数列{an}是公差为d的等差数列，数列{bn}是公比为q的(q∈R且q≠1)的等比数列，若函数f(x)=(x－1)2，且a1=f(d－1)，a3=f(d+1)，b1=f(q+1)，b3=f(q－1)，
(1)求数列{an}和{bn}的通项公式；
(2)设数列{cn}的前n项和为Sn，对一切n∈N*，都有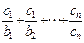
=an+1成立，求
，
，求
.
，
是否是等差数列
:
中的项，若是，是第几项？
满足
，
，试写出该数列的前
项，并用观察法写出这个数列的一个通项公式.
中，
，
，通项
是项数
的一次函数，
；
是由
组成，试归纳
.
；
时，利用以上结果求
的值.推荐套卷
已知数列{an}是公差为d的等差数列，数列{bn}是公比为q的(q∈R且q≠1)的等比数列，若函数f(x)=(x－1)2，且a1=f(d－1)，a3=f(d+1)，b1=f(q+1)，b3=f(q－1)，
(1)求数列{an}和{bn}的通项公式；
(2)设数列{cn}的前n项和为Sn，对一切n∈N*，都有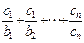=an+1成立，求
粤公网安备 44130202000953号