已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求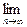 xn
xn
推荐套卷
已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求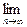 xn
xn