已知函数y=f(x)=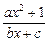 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.
(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由.
推荐套卷
已知函数y=f(x)=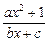 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< .
.
(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由.