已知{an}是等差数列，d为公差且不为0，a1和d均为实数，它的前n项和记作Sn,设集合A={(an,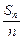
)|n∈N*},B={(x,y)|
x2－y2=1,x,y∈R}.
试问下列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明
(1)若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；
(2)A∩B至多有一个元素；
(3)当a1≠0时，一定有A∩B≠
.
相关试题
（其中
）的图象与
轴的交点中，相邻两个交点之间的距离为
，且图象上一个最低点为
，
的解析式 (2).当
时，求
，其中
，
是
上的减函数；
中，内角
对边的边长分别是
，已知
，
，求
；
，求
．
的解集；
，使
，求实数的取值范围．相关知识点
推荐套卷
已知{an}是等差数列，d为公差且不为0，a1和d均为实数，它的前n项和记作Sn,设集合A={(an,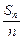)|n∈N*},B={(x,y)| x2－y2=1,x,y∈R}.
试问下列结论是否正确，如果正确，请给予证明；如果不正确，请举例说明
(1)若以集合A中的元素作为点的坐标，则这些点都在同一条直线上；
(2)A∩B至多有一个元素；
(3)当a1≠0时，一定有A∩B≠.
粤公网安备 44130202000953号