某电视台的一个智力游戏节目中，有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线．每连对一个得3分，连错得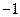
分，一名观众随意连线，他的得分记作ξ．
(1)求该观众得分ξ为非负的概率；
(2)求ξ的分布列及数学期望．
相关试题
判断方程
有
，
；
中，
侧面
，已知
；
(不包含端点
上确定一点
的位置,
；
的平面角的正切值.
的周期为
.
时，求
的取值范围；相关知识点
推荐套卷
某电视台的一个智力游戏节目中，有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目，每本名著只能与一名作者连线，每名作者也只能与一本名著连线．每连对一个得3分，连错得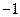分，一名观众随意连线，他的得分记作ξ．
(1)求该观众得分ξ为非负的概率；
(2)求ξ的分布列及数学期望．
粤公网安备 44130202000953号