已知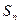 为数列
为数列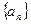 的前
的前 项和,
项和, ,
,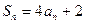 .
.
⑴设数列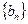 中,
中, ,求证:
,求证: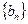 是等比数列;
是等比数列;
⑵设数列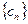 中,
中,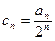 ,求证:
,求证: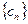 是等差数列;
是等差数列;
⑶求数列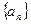 的通项公式及前
的通项公式及前 项和.
项和.
【解题思路】由于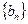 和
和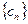 中的项与
中的项与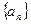 中的项有关,且
中的项有关,且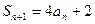 ,可利用
,可利用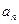 、
、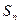 的关系作为切入点.
的关系作为切入点.
推荐套卷
已知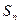 为数列
为数列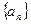 的前
的前 项和,
项和, ,
,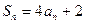 .
.
⑴设数列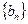 中,
中, ,求证:
,求证: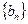 是等比数列;
是等比数列;
⑵设数列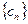 中,
中,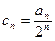 ,求证:
,求证: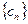 是等差数列;
是等差数列;
⑶求数列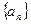 的通项公式及前
的通项公式及前 项和.
项和.
【解题思路】由于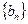 和
和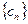 中的项与
中的项与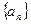 中的项有关,且
中的项有关,且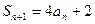 ,可利用
,可利用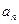 、
、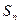 的关系作为切入点.
的关系作为切入点.