一机器可以按各种不同的速度运转，其生产物件有一些会有缺点，每小时生产有缺点物件的多少随机器运转速度而变化，用x表示转速（单位：转/秒），用y表示每小时生产的有缺点物件个数，现观测得到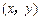
的4组观测值为（8，5），（12，8），（14，9），（16，11）．
（1）假定y与x之间有线性相关关系，求y对x的回归直线方程；
（2）若实际生产中所容许的每小时最大有缺点物件数为10，则机器的速度不得超过多少转/秒．（精确到1转/秒）
相关试题
为实常数）．
时，求函数
在
上的最小值；
在区间
上有解，求实数
的取值范围；
）
的表达式（不需证明）；
的最大值为
，
，求
的最小值.
在
上递增，求
的取值范围；
上的存在单调递减区间 ，求
（
），
的最小值；
，
：关于
的不等式
对任意
：函数
是增函数．若“
的取值范围．
（其中
）的图象与
轴的交点中，相邻两个交点之间的距离为
，且图象上一个点为
．
的解析式；
求函数
的图象向左平移推荐套卷
一机器可以按各种不同的速度运转，其生产物件有一些会有缺点，每小时生产有缺点物件的多少随机器运转速度而变化，用x表示转速（单位：转/秒），用y表示每小时生产的有缺点物件个数，现观测得到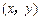的4组观测值为（8，5），（12，8），（14，9），（16，11）．
（1）假定y与x之间有线性相关关系，求y对x的回归直线方程；
（2）若实际生产中所容许的每小时最大有缺点物件数为10，则机器的速度不得超过多少转/秒．（精确到1转/秒）
粤公网安备 44130202000953号