(本小题满分14分)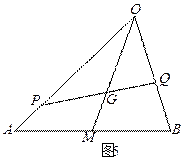 如图5,
如图5,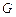 是△
是△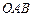 的重心,
的重心,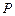 、
、 分别是边
分别是边 、
、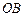 上的动点,且
上的动点,且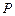 、
、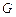 、
、 三点共线.(1)设
三点共线.(1)设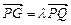 ,将
,将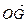 用
用 、
、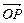 、
、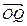 表示;
表示;
(2)设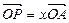 ,
,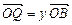 ,证明:
,证明: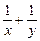 是定值;
是定值;
(3)记△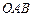 与△
与△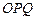 的面积分别为
的面积分别为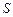 、
、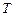 .求
.求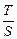 的取值范围.
的取值范围.
推荐套卷
(本小题满分14分)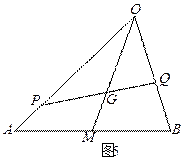 如图5,
如图5,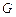 是△
是△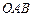 的重心,
的重心,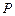 、
、 分别是边
分别是边 、
、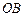 上的动点,且
上的动点,且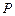 、
、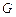 、
、 三点共线.(1)设
三点共线.(1)设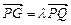 ,将
,将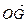 用
用 、
、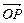 、
、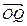 表示;
表示;
(2)设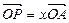 ,
,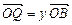 ,证明:
,证明: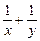 是定值;
是定值;
(3)记△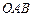 与△
与△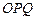 的面积分别为
的面积分别为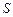 、
、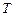 .求
.求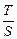 的取值范围.
的取值范围.