甲、乙两人各抛掷一次正方体骰子（它们的六个面分别标有数字
），设甲、乙所抛掷骰子朝上的面的点数分别为
、
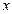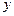，那么
（I）共有多少种不同的结果？
（II）请列出满足复数
的实部大于虚部的所有结果.
（III）满足复数的实部大于虚部的概率是多少？
相关试题
与向量
不可能平行；
，且
，求
的值.
满足：
，且
是
的等差中项.
，
，求使
成立的正整数
的最小值.
中，
，
平面
，
为
的中点，
，
．
；
为
的中点，求证：平面
平面
．
，向量
，函数
.
的最小正周期
；
分别为
内角
的对边，
为锐角，
，
恰是
上的最大值，求
.
的前
项和为
，且2
．
的通项公式；
求数列
的前推荐套卷
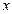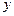甲、乙两人各抛掷一次正方体骰子（它们的六个面分别标有数字），设甲、乙所抛掷骰子朝上的面的点数分别为、，那么
（I）共有多少种不同的结果？
（II）请列出满足复数的实部大于虚部的所有结果.
（III）满足复数的实部大于虚部的概率是多少？
粤公网安备 44130202000953号