如图甲，在平面四边形ABCD中，已知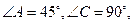
,
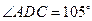,现将四边形ABCD沿BD折起，
使平面ABD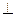
平面BDC（如图乙），设点E、F分别为棱
AC、AD的中点.
（1）求证：DC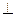平面ABC；
（2）求BF与平面ABC所成角的正弦；
（3）求二面角B－EF－A的余弦.
|
|||
|
|||
相关试题
的首项
，
，前
项和为
．
及
，
，求
的最大值．
中，内角
的对边分别为
，且
．
的大小；
，求
的值．
在
上单调递减且满足
.
的取值范围.
，求
在
中，角
，
，
对应的边分别是
，已知
.
的面积
，求
的值.
.
的最小正周期及最大值；
,且
，求
的值.推荐套卷
如图甲，在平面四边形ABCD中，已知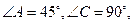
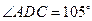,,现将四边形ABCD沿BD折起，
使平面ABD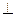平面BDC（如图乙），设点E、F分别为棱
AC、AD的中点.
（1）求证：DC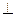平面ABC；
（2）求BF与平面ABC所成角的正弦；
（3）求二面角B－EF－A的余弦.
|
|||
|
|||
粤公网安备 44130202000953号