(本题满分14分)设等比数列 的首项为
的首项为 ,公比
,公比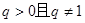 ,前
,前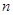 项和为
项和为
(Ⅰ)当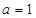 时,
时, 三数成等差数列,求数列
三数成等差数列,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数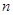 ,命题甲:
,命题甲: 三数构成等差数列.
三数构成等差数列.
命题乙: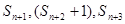 三数构成等差数列.
三数构成等差数列.
求证:对于同一个正整数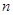 ,命题甲与命题乙不能同时为真命题.
,命题甲与命题乙不能同时为真命题.
推荐套卷
(本题满分14分)设等比数列 的首项为
的首项为 ,公比
,公比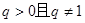 ,前
,前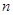 项和为
项和为
(Ⅰ)当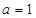 时,
时, 三数成等差数列,求数列
三数成等差数列,求数列 的通项公式;
的通项公式;
(Ⅱ)对任意正整数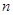 ,命题甲:
,命题甲: 三数构成等差数列.
三数构成等差数列.
命题乙: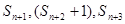 三数构成等差数列.
三数构成等差数列.
求证:对于同一个正整数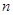 ,命题甲与命题乙不能同时为真命题.
,命题甲与命题乙不能同时为真命题.