已知y = f (x)是定义在[–1，1]上的奇函数，x∈[0，1]时，f (x) =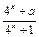
．
（1）求x∈[–1，0)时，y = f (x)解析式，并求y = f (x)在[0，1]上的最大值．
（2）解不等式f (x)>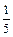
．
是一个等差 数列，且
。
； （2）求
项和
的最大值。
的三个内角，他们的对边分别为a、b、c，且
。
求bc的值，并求
的最大值。
的解集。
是直线
被椭圆
所截得的线段中点，求直线推荐套卷
已知y = f (x)是定义在[–1，1]上的奇函数，x∈[0，1]时，f (x) =．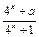
（1）求x∈[–1，0)时，y = f (x)解析式，并求y = f (x)在[0，1]上的最大值．
（2）解不等式f (x)>．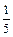
粤公网安备 44130202000953号