（本小题12分）
（改编题）(理)
四个纪念币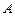
、
、
、
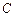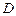,投掷时正面向上的概率如下表所示
.
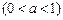| 纪念币 |
A |
B |
C |
D |
| 概率 |
 |
|
a |
a |
这四个纪念币同时投掷一次,设
表示出现正面向上的个数.
(Ⅰ)求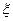
的分布列及数学期望；
(Ⅱ)在概率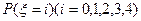
中,若
的值最大,求
的取值范围；
相关试题
与
是两个单位向量，其夹角为60°，且
，
的模；
，
都是锐角，
，
，求
的值
的终边与单位圆交于点P（
，
）.
、
、
值；
的值.
的前n项和。当
时，
的通项公式；试用n和
表示
，证明：
时，证明
，以A、B为焦点的椭圆经过点C。
与椭圆交于不同两点M、N，使
？若存在，求出直线
，存在不平行于x轴的直线
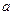，试求实数n的取值范围。推荐套卷
（本小题12分）
（改编题）(理)
四个纪念币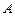、、、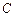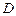,投掷时正面向上的概率如下表所示.
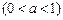| 纪念币 |
A |
B |
C |
D |
| 概率 |
|
|
a |
a |
这四个纪念币同时投掷一次,设表示出现正面向上的个数.
(Ⅰ)求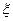的分布列及数学期望；
(Ⅱ)在概率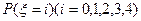中,若的值最大,求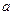的取值范围；
粤公网安备 44130202000953号