栽培甲、乙两种果树，先要培育成苗，然后再进行移栽．已知甲、乙两种果树成苗的概率分别为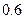
，
，移栽后成活的概率分别为
，
．
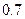（1）求甲、乙两种果树至少有一种果树成苗的概率；
（2）求恰好有一种果树能培育成苗且移栽成活的概率．
相关试题
，
．
是等比数列；
的成立的n的集合．
．
的最大值，并求取得最大值时角A、B的大小．
，且
为锐角，求：
的值；
的值．
．
中，
，求其第4项及前5项和.相关知识点
推荐套卷
栽培甲、乙两种果树，先要培育成苗，然后再进行移栽．已知甲、乙两种果树成苗的概率分别为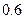，，移栽后成活的概率分别为，．
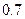（1）求甲、乙两种果树至少有一种果树成苗的概率；
（2）求恰好有一种果树能培育成苗且移栽成活的概率．
粤公网安备 44130202000953号