某学校共有教师
人，其中不到
岁的有
人，岁及以上的有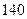
人。为了了解普通话在该校中的推广普及情况，用分层抽样的方法，从全体教师中抽取一个容量为
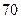人的样本进行普通话水平测试，其中在不到岁的教师中应抽取的人数为多少人？
相关试题
;
.
,b=9.求：
.
≤a≤相关知识点
推荐套卷
某学校共有教师人，其中不到岁的有人，岁及以上的有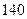人。为了了解普通话在该校中的推广普及情况，用分层抽样的方法，从全体教师中抽取一个容量为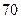人的样本进行普通话水平测试，其中在不到岁的教师中应抽取的人数为多少人？
粤公网安备 44130202000953号