如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC＝BC＝CC1，M、N分别是A1B、B1C1的中点.
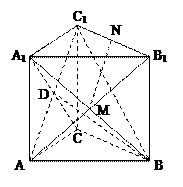
（Ⅰ）求证：MN⊥平面A1BC；
（Ⅱ）求直线BC1和平面A1BC所成角的大小.
的顶点与直角坐标系的原点重合，始边在
轴的非负半轴上，终边经过点
，求
的值
中，已知内角
,边
，设内角
，周长为
.
的解析式；
和
的图象上相邻的最高点与最低点的坐标分别为M（
，求此函数的解析式
+
)的图像，请写出变换过程，并画出一个周期的闭区间的函数简图推荐套卷
如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，AC＝BC＝CC1，M、N分别是A1B、B1C1的中点.
（Ⅰ）求证：MN⊥平面A1BC；
（Ⅱ）求直线BC1和平面A1BC所成角的大小.
粤公网安备 44130202000953号