甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约.乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设甲面试合格的概率为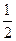
，乙、丙面试合格的概率都是
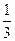，且面试是否合格互不影响．求：
（1）至少有1人面试合格的概率;（2）签约人数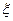
的分布列和数学期望．
相关试题
=(4,2).
在
上是增函数，且
的解析式；
＜0.
的递增区间是
的值。
，求
在区间
上的最大值和最小值。
在
上递增，函数f（x）的一个零点为
，
的x的取值集合.
相关知识点
推荐套卷
甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约.乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设甲面试合格的概率为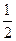，乙、丙面试合格的概率都是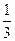，且面试是否合格互不影响．求：
（1）至少有1人面试合格的概率;（2）签约人数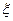的分布列和数学期望．
粤公网安备 44130202000953号