对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数
f(x)=ax2+bx+1(a>0)有两个相异的不动点x1,x2.
⑴若x1<1<x2,且f(x)的图象关于直线x=m对称,求证: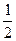 <m<1;
<m<1;
⑵若|x1|<2且|x1-x2|=2,求b的取值范围.
相关知识点
推荐套卷
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数
f(x)=ax2+bx+1(a>0)有两个相异的不动点x1,x2.
⑴若x1<1<x2,且f(x)的图象关于直线x=m对称,求证: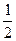 <m<1;
<m<1;
⑵若|x1|<2且|x1-x2|=2,求b的取值范围.