如图，甲船以每小时
海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于
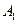处时，乙船位于甲船的北偏西
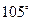方向的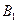
处，此时两船相距
海里，当甲船航行分钟到达
处时，乙船航行到甲船的北偏西
方向的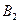
处，此时两船相距
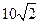海里，问乙船每小时航行多少海里？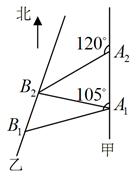
相关试题
的公差为d，前
项和为
，等比数列
的公比为
．已知
，
，
，
．
时，记
，求数列
的前
．
的前
项和
，且
成等差数列．
的前n项和
，求得
成立的n的最小值．
中，
求数列
证明：
满足
，且
成等差数列．
的值和
，求数列
的前
项和．
，
是曲线
在点
处的切线与x轴交点的横坐标．
的通项公式；
，证明
．推荐套卷
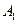如图，甲船以每小时海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于处时，乙船位于甲船的北偏西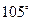方向的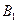处，此时两船相距海里，当甲船航行分钟到达处时，乙船航行到甲船的北偏西方向的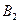处，此时两船相距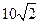海里，问乙船每小时航行多少海里？
粤公网安备 44130202000953号