某车队2008年初以98万元购进一辆大客车,并投入营运,第一年需支出各种费用12万元,从第二年起每年支出费用均比上一年增加4万元,该车投入营运后每年的票款收入为50万元,设营运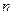 年该车的盈利总额为
年该车的盈利总额为 万元.
万元.
(1)写出 关于
关于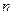 的函数关系式; (2)从哪一年开始,该汽车开始获利; (3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
的函数关系式; (2)从哪一年开始,该汽车开始获利; (3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
方案2——当年均盈利额最大时,年底以40万元的价格卖掉该车.试问车队以哪种方案处理该车获利较大?
推荐套卷
某车队2008年初以98万元购进一辆大客车,并投入营运,第一年需支出各种费用12万元,从第二年起每年支出费用均比上一年增加4万元,该车投入营运后每年的票款收入为50万元,设营运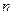 年该车的盈利总额为
年该车的盈利总额为 万元.
万元.
(1)写出 关于
关于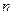 的函数关系式; (2)从哪一年开始,该汽车开始获利; (3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
的函数关系式; (2)从哪一年开始,该汽车开始获利; (3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
方案2——当年均盈利额最大时,年底以40万元的价格卖掉该车.试问车队以哪种方案处理该车获利较大?