（本小题满分12分）如图所示，△ABC中，∠A=60°、∠C=45°，BC=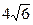
，现点D在AC边上运动，点E在AB边上运动（不与端点重合）且AD=BE=
，设△ADE面积为S
（1）写出函数式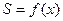
，并标出定义域。
（2）求出取何值时，S有最大值，并求之。
相关试题
=
.
=
在[-2,
]恰有2解，求实数
的取值范围.
}是等差数列，
=4，其前10项和
=100，数列{
}满足
.
，求数列{
}的前n项和
．
中，
,
,
分别是△
,
,
的对边，
.
+
)的取值范围.
= 
（A>0，
）的图像如图所示.
，
，
；
=
，若对任意的
，都有
，求
的取值范围.
：关于
的不等式
＜
无解；命题
：函数
=
的值域为R.若“相关知识点
推荐套卷
（本小题满分12分）如图所示，△ABC中，∠A=60°、∠C=45°，BC=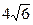，现点D在AC边上运动，点E在AB边上运动（不与端点重合）且AD=BE=，设△ADE面积为S
（1）写出函数式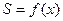，并标出定义域。
（2）求出取何值时，S有最大值，并求之。
粤公网安备 44130202000953号