(本小题满分10分)如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为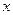 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为 ,
,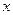 、
、

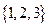 ,设
,设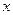 +
+ 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为 .
.
(Ⅰ)求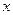 <2且
<2且 >1的概率;
>1的概率;
(Ⅱ)某人进行了12次游戏,求他平均可以得到的奖励分.
推荐套卷
(本小题满分10分)如图是两个独立的转盘(A)、(B),在两个图中三个扇形区域的圆心角分别为60°、120°、180°。用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为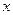 ,转盘(B)指针所对的区域为
,转盘(B)指针所对的区域为 ,
,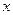 、
、

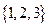 ,设
,设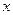 +
+ 的值为
的值为 ,每一次游戏得到奖励分为
,每一次游戏得到奖励分为 .
.
(Ⅰ)求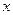 <2且
<2且 >1的概率;
>1的概率;
(Ⅱ)某人进行了12次游戏,求他平均可以得到的奖励分.