关于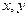 的方程
的方程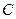 :
: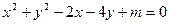 . (1)若方程
. (1)若方程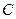 表示圆,求实数
表示圆,求实数 的范围;(2)在方程
的范围;(2)在方程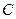 表示圆时,若该圆与直线
表示圆时,若该圆与直线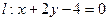 相交于
相交于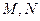 两点,且
两点,且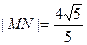 ,求实数
,求实数 的值;(3)在(2)的条件下,若定点
的值;(3)在(2)的条件下,若定点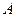 的坐标为(1,0),点
的坐标为(1,0),点 是线段
是线段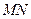 上的动点,求直线
上的动点,求直线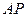 斜率的取值范围.
斜率的取值范围.
相关知识点
推荐套卷
关于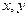 的方程
的方程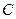 :
: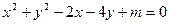 . (1)若方程
. (1)若方程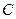 表示圆,求实数
表示圆,求实数 的范围;(2)在方程
的范围;(2)在方程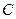 表示圆时,若该圆与直线
表示圆时,若该圆与直线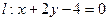 相交于
相交于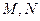 两点,且
两点,且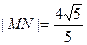 ,求实数
,求实数 的值;(3)在(2)的条件下,若定点
的值;(3)在(2)的条件下,若定点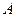 的坐标为(1,0),点
的坐标为(1,0),点 是线段
是线段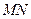 上的动点,求直线
上的动点,求直线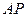 斜率的取值范围.
斜率的取值范围.