(本题满分12分)设A(x
，y
)、B(x，y) 是椭圆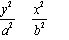
(a > b > 0) 上的两点，
，
= (
，
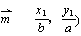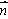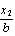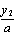)，且满足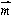
·
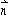= 0，椭圆的离心率e = 
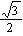，短轴长为2，O为坐标原点．(1)求椭圆的方程；(2)若存在斜率为k的直线AB过椭圆的焦点F(0，c)(c为半焦距)，求直线AB的斜率k的值．
相关试题
中，
分别为内角
的对边，且
的大小；
，试求内角B、C的大小．
的前n项和为
.已知
求
和
是一个公差大于0的等差数列，且满足
．
满足：
，若数列
，求数列
的前n项和
．
,
分别是椭圆E：
+
=1（0﹤b﹤1）的左、右焦点，过
与E相交于A、B两点，且
，
，
成等差数列。
中，
分别为内角
的对边，且
的大小；
，试求内角B、C的大小．推荐套卷
(本题满分12分)设A(x，y)、B(x，y) 是椭圆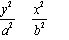(a > b > 0) 上的两点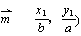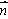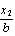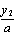，， = (，)，且满足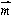· 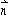= 0，椭圆的离心率e = 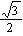，短轴长为2，O为坐标原点．(1)求椭圆的方程；(2)若存在斜率为k的直线AB过椭圆的焦点F(0，c)(c为半焦距)，求直线AB的斜率k的值．
粤公网安备 44130202000953号