甲、乙等五名奥运志愿者被随机地分到A、B、C、D四个不同的岗位服务，每个岗位至少有一名志愿者
（1）求甲、乙两人同时参加A岗位服务的概率
（2）求甲、乙两人不在同一个岗位服务的概率
（3）设随机变量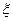
为这5名志愿者中参加A岗位服务的人数，求
相关试题
是单位圆
上的点，点
是单位圆与
轴正半轴的交点，点
在第二象限．记
且
．
的值．
的不等式
的解集是空集，求实数
的取值范围
都是正数．
，求
的最大值；
，求
的最小值．
．
的单调递增区间；
的方程
在
]上有两个不同的解，求实数
的取值范围．推荐套卷
甲、乙等五名奥运志愿者被随机地分到A、B、C、D四个不同的岗位服务，每个岗位至少有一名志愿者
（1）求甲、乙两人同时参加A岗位服务的概率
（2）求甲、乙两人不在同一个岗位服务的概率
（3）设随机变量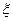为这5名志愿者中参加A岗位服务的人数，求
粤公网安备 44130202000953号