已知直线l的方程为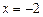
，且直线l与x轴交于点M，圆
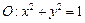与x轴交于
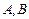两点（如图）．
（I）过M点的直线
交圆于
两点，且圆孤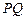
恰为圆周的
，求直线的方程；
（II）求以l为准线，中心在原点，且与圆O恰有两个公共点的椭圆方程；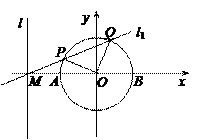
（III）过M点的圆的切线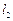
交（II）中的一个椭圆于
两点，其中两点在x轴上方，求线段CD的长．
相关试题
与平面
且平行于平面
的一个截面，并说明理由；
的值；
(其中
是
的最大值；
时，求证：
.
（万元）与每件产品的售价
出
的切线，求此直线方程.推荐套卷
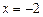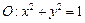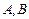已知直线l的方程为，且直线l与x轴交于点M，圆与x轴交于两点（如图）．
（I）过M点的直线交圆于两点，且圆孤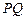恰为圆周的，求直线的方程；
（II）求以l为准线，中心在原点，且与圆O恰有两个公共点的椭圆方程；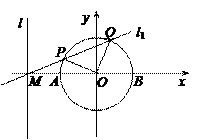
（III）过M点的圆的切线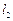交（II）中的一个椭圆于两点，其中两点在x轴上方，求线段CD的长．
粤公网安备 44130202000953号