(本小题满分13分)某隧道长2150m,通过隧道的车速不能超过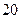 m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为
m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为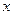 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当 时,相邻两车之间保持20 m的距离;当
时,相邻两车之间保持20 m的距离;当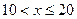 时,相邻两车之间保持
时,相邻两车之间保持 m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为 . (I)将
. (I)将 表示为
表示为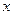 的
的 函数;(II)求车队通过隧道时间
函数;(II)求车队通过隧道时间 的最小值及此时车队的速度.
的最小值及此时车队的速度.
推荐套卷
(本小题满分13分)某隧道长2150m,通过隧道的车速不能超过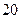 m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为
m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为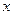 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当 时,相邻两车之间保持20 m的距离;当
时,相邻两车之间保持20 m的距离;当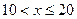 时,相邻两车之间保持
时,相邻两车之间保持 m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为 . (I)将
. (I)将 表示为
表示为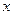 的
的 函数;(II)求车队通过隧道时间
函数;(II)求车队通过隧道时间 的最小值及此时车队的速度.
的最小值及此时车队的速度.