(本题满分13分)已知y= F(x)的导函数为f(x)=ax3+bx2+cx+d(a≠0),
函数y=f(x)的图象如右图所示，且函数y=F(x)的图象经过（1，2）和（－1，2）两点，又过点（1，0）作斜率之积为－10的两条直线l1和l2，l1和l2与函数
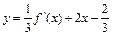的图象分别相交于A、B两点和C、D两点，O为坐标原点。
（1）求函数y=f(x)的对称中心的坐标；
（2）若线段AB和CD的中点分别为M，N，求三角OMN面积的取值范围。
相关试题
（n∈N*）,它的前n项和为
，且
求数列
+
的最小值；
+
+
的最小值．
时，求f（x）的极值点；
+
=1有相同焦点，且经过点（4，
）．推荐套卷
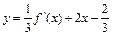(本题满分13分)已知y= F(x)的导函数为f(x)=ax3+bx2+cx+d(a≠0),函数y=f(x)的图象如右图所示，且函数y=F(x)的图象经过（1，2）和（－1，2）两点，又过点（1，0）作斜率之积为－10的两条直线l1和l2，l1和l2与函数的图象分别相交于A、B两点和C、D两点，O为坐标原点。
（1）求函数y=f(x)的对称中心的坐标；
（2）若线段AB和CD的中点分别为M，N，求三角OMN面积的取值范围。
粤公网安备 44130202000953号