已知椭圆C：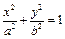
(a＞b＞0)的左准线恰为抛物线E：y2 = 16x的准线，直线l：x + 2y – 4 = 0与椭圆相切．（1）求椭圆C的方程；（2）如果椭圆C的左顶点为A，右焦点为F，过F的直线与椭圆C交于P、Q两点，直线AP、AQ与椭圆C的右准线分别交于N、M两点，求证：四边形MNPQ的对角线的交点是定点．
相关试题
，
．
时，求函数
的最小值；
恒成立，试求实数
中，
分别为
的对边,已知
．
；
，
时，求
是递增的等差数列，
．
，求数列
的前n项和
．
.
，且
在
上单调递增，求实数
的取值范围；
时，有
.若对于任意的实数
，存在最大的实数
，使得当
时，
恒成立，试求用
的公差不为零,
,等比数列
的前3项满足
.
…
，是否存在最大整数
，使对任意的
，均有
总成立?若存在,求出推荐套卷
已知椭圆C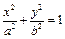：(a＞b＞0)的左准线恰为抛物线E：y2 = 16x的准线，直线l：x + 2y – 4 = 0与椭圆相切．（1）求椭圆C的方程；（2）如果椭圆C的左顶点为A，右焦点为F，过F的直线与椭圆C交于P、Q两点，直线AP、AQ与椭圆C的右准线分别交于N、M两点，求证：四边形MNPQ的对角线的交点是定点．
粤公网安备 44130202000953号