（本小题满分16分）已知F1（－c,0）, F2（c,0） (c＞0)是椭圆的两个焦点，O为坐标原点，圆M的方程是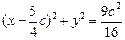
．
（1）若P是圆M上的任意一点，求证：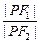
是定值；
（2）若椭圆经过圆上一点Q，且cos∠F1QF2=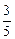
，求椭圆的离心率；
（3）在（2）的条件下，若|OQ|=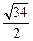
，求椭圆的方程．
推荐套卷
（本小题满分16分）已知F1（－c,0）, F2（c,0） (c＞0)是椭圆的两个焦点，O为坐标原点，圆M的方程是．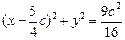
（1）若P是圆M上的任意一点，求证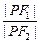：是定值；
（2）若椭圆经过圆上一点Q，且cos∠F1QF2=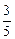，求椭圆的离心率；
（3）在（2）的条件下，若|OQ|=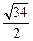，求椭圆的方程．
粤公网安备 44130202000953号