（几何证明选讲）
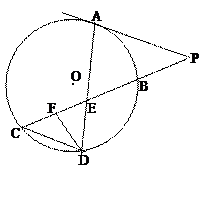
如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF·EC.
(1)求证：ÐP=ÐEDF；
(2)求证：CE·EB=EF·EP；
(3)若CE : BE="3" : 2，DE=6，EF= 4，求PA的长.
,A、B是U的子集,同时满足
求A和B .
,
且
求
的值.
,则
.
求A;
求
的值.
,若
求实数
的值.推荐套卷
（几何证明选讲）
如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF·EC.
(1)求证：ÐP=ÐEDF；
(2)求证：CE·EB=EF·EP；
(3)若CE : BE="3" : 2，DE=6，EF= 4，求PA的长.
粤公网安备 44130202000953号