（本小题12分）设点
，点A在y轴上移动，点B在x轴正半轴（包括原点）上移动，点M在AB连线上，且满足
，
．
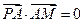（Ⅰ）求动点M的轨迹C的方程；
（Ⅱ）设轨迹C的焦点为F，准线为l，自M引的垂线，垂足为N，设点
使四边形PFMN是菱形，试求实数a；
（Ⅲ）如果点A的坐标为
，
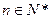，其中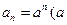
＞
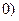，相应线段AM的垂直平分线交x轴于
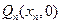．设数列
的前n项和为
，证明：当n≥2时，
为定值．
相关试题
中，角
所对的边为
．已知
，且
．
的值；
时，求
．
为等差数列
的前
项和，已知
．
；
．
．
时，求
在区间
上的最值；
时，有
恒成立，求
的取值范围．
为自然对数的底数
．
的最小值；
对任意的
恒成立，求实数
的值．
．
的单调区间；
时，
恒成立，求实数
的取值范围．推荐套卷
（本小题12分）设点，点A在y轴上移动，点B在x轴正半轴（包括原点）上移动，点M在AB连线上，且满足，．
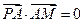（Ⅰ）求动点M的轨迹C的方程；
（Ⅱ）设轨迹C的焦点为F，准线为l，自M引的垂线，垂足为N，设点使四边形PFMN是菱形，试求实数a；（Ⅲ）如果点A的坐标为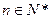，，其中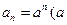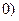＞，相应线段AM的垂直平分线交x轴于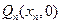．设数列的前n项和为，证明：当n≥2时，为定值．
粤公网安备 44130202000953号