（本小题满分12分）
（理）已知Sn是正数数列{an}的前n项和，S12，S22、……、Sn2 ……，是以3为首项，以1为公差的等差数列；数列{bn}为无穷等比数列，其前四项之和为120，第二项与第四项之和为90．
(I)求an、bn；(II)从数列{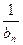
}中能否挑出唯一的无穷等比数列，使它的各项和等于
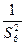．若能的话，请写出这个数列的第一项和公比?若不能的话，请说明理由．
(i为虚数单位)
，△ABC的面积为
。
=
。若
。
（x∈R）的值域。
满足
为虚数单位），
，求一个以
为根的实系数一元二次方程.
.推荐套卷
（本小题满分12分）
（理）已知Sn是正数数列{an}的前n项和，S12，S22、……、Sn2 ……，是以3为首项，以1为公差的等差数列；数列{bn}为无穷等比数列，其前四项之和为120，第二项与第四项之和为90．
(I)求an、bn；(II)从数列{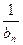}中能否挑出唯一的无穷等比数列，使它的各项和等于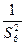．若能的话，请写出这个数列的第一项和公比?若不能的话，请说明理由．
粤公网安备 44130202000953号