(本小题满分14分)已知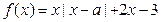 (Ⅰ)当
(Ⅰ)当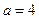 ,
,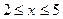 时,问
时,问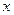 分别取何值时,函数
分别取何值时,函数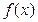 取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若
取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若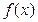 在R上恒为增函数,试求
在R上恒为增函数,试求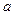 的取值范围;
的取值范围;
(Ⅲ)已知常数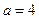 ,数列
,数列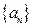 满足
满足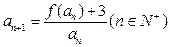 ,试探求
,试探求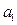 的值,使得数列
的值,使得数列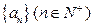 成等差数列.
成等差数列.
相关知识点
推荐套卷
(本小题满分14分)已知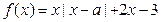 (Ⅰ)当
(Ⅰ)当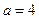 ,
,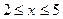 时,问
时,问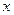 分别取何值时,函数
分别取何值时,函数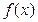 取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若
取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若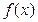 在R上恒为增函数,试求
在R上恒为增函数,试求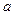 的取值范围;
的取值范围;
(Ⅲ)已知常数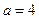 ,数列
,数列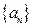 满足
满足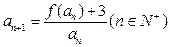 ,试探求
,试探求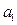 的值,使得数列
的值,使得数列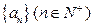 成等差数列.
成等差数列.