（本小题满分12分）
四个大小相同的小球分别标有数字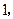
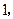
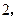
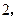把它们放在一个盒子中，从中任意摸出两个小球，它们的标号分别为
、
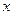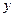，记随机变量
.
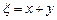（1）求随机变量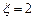
时的概率；
（2）求随机变量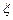
的概率分布列及数学期望。
相关试题
，
，
，试求点
的坐标，使四边形
为等腰梯形．
，
的直线
的倾斜角为45度，求
的值．
的物体时，长20 cm．在弹性限度内，所挂物体的重量每增加
，弹簧就伸长
cm．试写出弹簧的长度
（cm）与所挂物体重量
之间的关系的方程．
相关知识点
推荐套卷
（本小题满分12分）
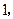
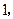
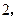
四个大小相同的小球分别标有数字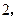把它们放在一个盒子中，从中任意摸出两个小球，它们的标号分别为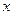、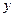，记随机变量.
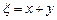（1）求随机变量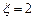时的概率；
（2）求随机变量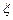的概率分布列及数学期望。
粤公网安备 44130202000953号