(本题满分14分)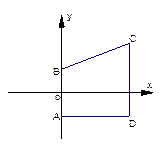
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
(3)设轨迹E与直线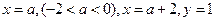 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
推荐套卷
(本题满分14分)
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
(3)设轨迹E与直线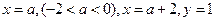 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。