将连续正整数从小到大排列构成一个数,为这个数的位数(如时,此数为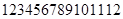 ,共有15个数字,),现从这个数中随机取一个数字,为恰好取到0的概率.
,共有15个数字,),现从这个数中随机取一个数字,为恰好取到0的概率.
(1)求;
(2)当时,求的表达式;
(3)令为这个数中数字0的个数,为这个数中数字9的个数,,,求当,时的最大值.
推荐套卷
将连续正整数从小到大排列构成一个数,为这个数的位数(如时,此数为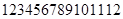 ,共有15个数字,),现从这个数中随机取一个数字,为恰好取到0的概率.
,共有15个数字,),现从这个数中随机取一个数字,为恰好取到0的概率.
(1)求;
(2)当时,求的表达式;
(3)令为这个数中数字0的个数,为这个数中数字9的个数,,,求当,时的最大值.